THERE’S A VERY good reason that humans are still using gas-powered cars. Despite the negative side effects of combustion—it releases not just energy, but carbon dioxide—the simple fact is that you can get more energy out of gasoline than you can from other energy sources. A typical car can travel 30 miles on just one gallon of gasoline. That’s crazy!
Soon enough, the oil that gasoline comes from will become too expensive to produce. But until then, cars running off of other forms of energy—like batteries—will need to battle against the impressive storage capacity of gasoline. So I want to focus on just how different that energy storage can be.
Instead of measuring the total energy stored, it’s best to consider the energy density—defined as the stored energy per unit volume in units of megajoules per liter. It’s just like mass density (mass per volume) except that we use energy instead of mass. Another common property of energy storage is the specific energy, the stored energy per mass (in megajoules per kilogram). But since I want to compare things to gasoline (which is usually measured in gallons), I’ll stick with energy density.
So let’s say I want to replace a liter of gasoline with some other energy storage stuff of the same volume. With different energy storage, how far could a liter of energy take a car? (Yes, I’m switching to volume units of liters instead of gallons but I am going to stick to distance in miles—crazy, right?) According to Wikipedia, gasoline, as an energy storage, has 34 megajoules per liter. Assuming a car efficiency of 25 percent, then of this 34 MJ only 8.5 MJ goes into moving the car. If a car gets 7.9 miles per liter (based on fuel efficiency) then I can get a ratio of energy per mile (based on the energy in the gasoline). This would be 8.5 MJ per 7.9 miles or 1.08 MJ/mile. This is the energy cost to drive a car—I’m going to assume it doesn’t depend on the energy source.
But what if I replace the gasoline engine with a lithium-ion battery and an electric motor? In this case, there are two things that change. First is the starting energy. A lithium-ion battery has an energy density of about 2 MJ/L (different batteries have different energy densities). Second is the efficiency. Since a battery with an electric motor doesn’t have to waste energy in the explosion of gasoline, it has an overall efficiency of about 50 percent. So, that 2 MJ in a 1 liter battery would be able to put about 1 MJ towards driving a car. The car will still have the same amount of energy loss to friction and air resistance so that this 1 MJ would be able to move the car about 1 mile (OK—actually it would be 0.93 miles).
As you can see, there might be lots of reasons to use an electric car instead of a gasoline powered car—but the driving range is not one of those reasons. There’s no denying it: There is a bunch of energy stored in gasoline.
OK, but what about replacing the battery with something else (coal, rubber bands, a ham and cheese sandwich, or plutonium)? I can repeat the above calculations using other energy storage materials. Here, I made a graph for you. Yes, I had to make some assumptions about efficiencies and also I had to estimate the energy density of a rubber band (I think I will save the details for a future post).
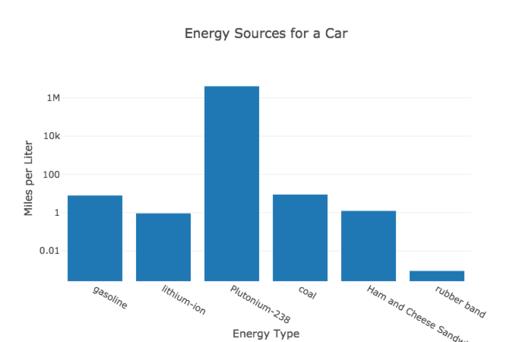
The vertical axis is a log-scale. I also hope you realize that even though plutonium has a very high energy density, it’s just not going to be in your car in the near future. But what about a sandwich? That seems like a good option for the future of cars.

